题目描述

欢迎来到麻州扑克的世界！这里充满了刺激和机遇，准备好迎接挑战了吗？

在麻州扑克中，我们使用了一副特殊的扑克牌。牌堆包含了点数 $1$ 到 $9$ 的条纹牌，分别有 $a_1, a_2, \ldots, a_9$ 张；同时也包含了点数为 $1$ 到 $9$ 的圆筒牌，分别有 $b_1, b_2, \ldots, b_9$ 张。一共有

$$\sum_{i=1}^{9} a_i + \sum_{i=1}^{9} b_i$$

张牌，下图是圆筒牌（第一行）和条纹牌（第二行）的样式示意图。

图 1：圆筒牌和条纹牌样式示意图

游戏规则如下：每局游戏开始时，庄家会先从一对、两对、三条、顺子、葫芦、四张、同花顺这七种牌型中选择一种作为目标牌型，接着庄家首先从牌堆中抽取五张牌作为庄家的手牌，而你将继续从牌堆中抽取两张牌作为你的手牌。你需要在庄家手牌的五张牌中选取三张牌（第一行）和你的两张牌（第二行）组合成你最终的牌型，下图是选取最终牌型的示意图。

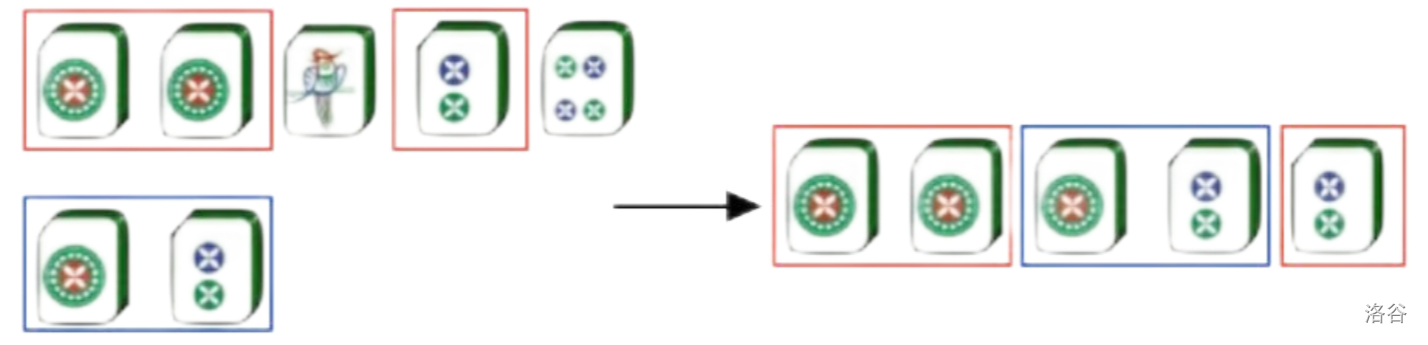图 2：最终牌型选取示意图

如果你的最终牌型与庄家开局时选择的目标牌型完全一致，则恭喜你获得胜利，将会获得巨额奖励！但是如果你的最终牌型与庄家开局选择的牌型不一致，则很遗憾你输了，将会面临严峻的惩罚。现在你非常想获得胜利，你的任务是计算给定庄家选择的目标牌型的情况下，你绝对聪明时获胜概率是多少。

以下是不同牌型的详细定义：

• 一对（Pair）：最终的牌型中有两张牌的点数相同，其他三张牌的点数互不相同且均与一对的点数不同，即点数形如 A A B C D，图 3 是一对这一牌型的示意图。

图 3：一对示意图

• 两对（Two_Pairs）：最终的牌型中有两对牌的点数都相同，且这两对牌之间的点数不同，剩余一张牌的点数与这两对的点数均不相同，即点数形如 A A B B C，图 4 是两对这一牌型的示意图。

图 4：两对示意图

• 三条（Three_of_a_Kind）：最终的牌型中有三张牌的点数相同，其他两张牌的点数互不相同且均与三条的点数不同，即点数形如 A A A B C，图 5 是三条这一牌型的示意图。

图 5：三条示意图

• 顺子（Straight）：手牌中的点数连续排列，且即有条纹牌也有圆筒牌，点数形如 A A+1 A+2 A+3 A+4，图 6 是顺子这一牌型的示意图。

图 6：顺子示意图

• 葫芦（Full_House）：手牌中有三张牌的点数相同，另外两张牌的点数也相同且不与三张牌的点数相同，即点数形如 A A A B B，图 7 是葫芦这一牌型的示意图。

图 7：葫芦示意图

• 四张（Four_of_a_Kind）：手牌中有四张牌的点数相同，另外一张牌点数不同，即点数形如 A A A A B，图 8 是四张这一牌型的示意图。

图 8：四张示意图

• 同花顺（Straight_Flush）：手牌中的点数连续排列，且只有条纹牌或只有圆筒牌，点数形如 A A+1 A+2 A+3 A+4，图 9 是同花顺这一牌型的示意图。

图 9：同花顺示意图

输入格式

第一行包含九个整数 $a_1, a_2, \ldots, a_9$，表示点数 $1$ 到 $9$ 的条纹牌的数量。

第二行包含九个整数 $b_1, b_2, \ldots, b_9$，表示点数 $1$ 到 $9$ 的圆筒牌的数量。

第三行字符串

$$S \in \{\text{Pair}, \text{Two\_Pairs}, \text{Three\_of\_a\_Kind}, \text{Straight}, \text{Full\_House}, \text{Four\_of\_a\_Kind}, \text{Straight\_Flush}\} $$

表示庄家开局时选择的目标牌型。

输出格式

输出共 $1$ 行，如果你绝对聪明时获胜的概率为最简分数 $\dfrac{x}{y}$，则需要输出 $x \cdot y^{-1} \bmod 998244353$，其中 $y^{-1}$ 表示 $y$ 在模 $998244353$ 意义下的逆元。

输入输出样例 #1

输入 #1

5 2 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
Four_of_a_Kind

输出 #1

380283564

说明/提示

对于 $100\%$ 的数据，满足

$$7 \leq \sum_{i=1}^{9} a_i + \sum_{i=1}^{9} b_i \leq 10^5. $$